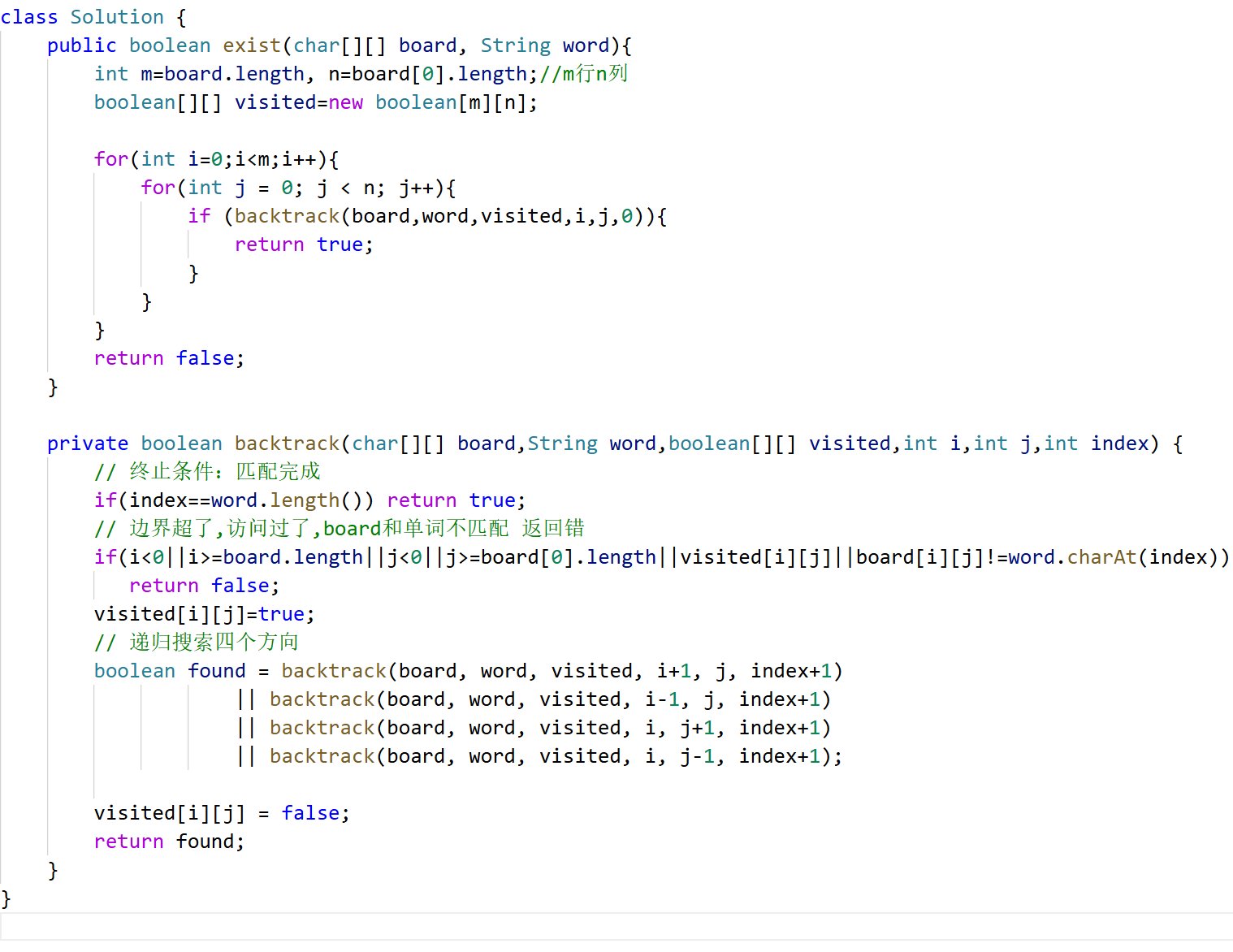
回溯算法说白了就是穷举法。所有回溯法解决的问题都可以抽象为树形结构,因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度就构成了树的深度。递归就要有终止条件,所以必然是一棵高度有限的树(N叉树)。
😚表示codetop里的高频题。
0.做题步骤
1.判断是不是用回溯
总体而言就是这道题必须要罗列所有的可能性才能得到答案。
可以解决的问题:对于一维数组有罗列组合,排列
组合问题:N个数里面按一定规则找出k个数的集合
切割问题:一个字符串按一定规则有几种切割方式
子集问题:一个N个数的集合里有多少符合条件的子集
排列问题:N个数按一定规则全排列,有几种排列方式
棋盘问题:N皇后,解数独等等
2.画树形图
这里看下面的回溯三部曲模板
3.套对应题型的模板
4.要去重吗?
1.总结
回溯函数里的参数要不要有startindex?
排列有顺序,所以不用startindex,每层都是从0开始搜素。
组合问题中:如果是一个集合的话,就需要startIndex。但如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex。
是不是在叶子节点里找答案?
组合 分割 排列 棋盘都是在叶子节点里找答案。叶子节点就是当收集元素的数组path的大小达到和nums数组一样大的时候,result add然后return。只有子集是在所有节点里找答案。回溯里不用判断return也ok。
判断逻辑复杂的都是另起一个子函数。
组合问题就最简单最基本。
切割问题有两种割法:1.用StringBuilder定义 2.substring截取
子集问题在所有节点里找答案,在回溯开头就要记录所有路径节点。
排列问题i初始都从0开始,而不是startindex;还有要用boolean的used数组记录那些值用过。
棋盘问题就是二维搜索,先for检索row,再检索col,在col里给值递归回溯撤销。
去重的两种类型
1.输入内容只能用一次
1.输入内容只能用一次,树枝去重,确保同一个元素在一条路径(树枝)中不会被重复使用。
去重实现方式:
(1)让递归的时候回溯函数中的startindex从i+1开始就够了。
(2)如果是排列问题不用startindex,那就用used标记判断:used[i - 1] == true就说明同一树枝candidates[i - 1]使用过,continue就完事。
2.输出内容不能重复
2.输出内容不能重复,树层去重,确保递归中同一层重复选择相同的值导致最后结果重复。
去重实现方式:
(1)排序后判断相邻元素:
组合子集切割问题:if (i > startIndex && nums[i] == nums[i-1]) continue。
排列问题:if (i > 0 && nums[i] == nums[i-1] && !used[i-1]) continue。
(2)不能排序使用hasp
性能分析 没太有用
1.子集问题分析:
时间复杂度:O(2n),因为每一个元素的状态无外乎取与不取,所以时间复杂度为O(2n)
空间复杂度:O(n),递归深度为n,所以系统栈所用空间为O(n),每一层递归所用的空间都是常数级别,注意代码里的result和path都是全局变量,就算是放在参数里,传的也是引用,并不会新申请内存空间,最终空间复杂度为O(n)
2.排列问题分析:
时间复杂度:O(n!),这个可以从排列的树形图中很明显发现,每一层节点为n,第二层每一个分支都延伸了n-1个分支,再往下又是n-2个分支,所以一直到叶子节点一共就是 n * n-1 * n-2 * … 1 = n!。
空间复杂度:O(n),和子集问题同理。
3.组合问题分析:
时间复杂度:O(2^n),组合问题其实就是一种子集的问题,所以组合问题最坏的情况,也不会超过子集问题的时间复杂度。
空间复杂度:O(n),和子集问题同理。
4.N皇后问题分析:
时间复杂度:O(n!) ,其实如果看树形图的话,直觉上是O(n^n),但皇后之间不能见面所以在搜索的过程中是有剪枝的,最差也就是O(n!),n!表示n * (n-1) * … * 1。
空间复杂度:O(n),和子集问题同理。
5.解数独问题分析:
时间复杂度:O(9^m) , m是’.'的数目。
空间复杂度:O(n2),递归的深度是n2
回溯三部曲模板
- 回溯函数模板返回值以及参数:我需要什么,需要返回什么
- 回溯函数终止条件:我什么时候停下
- 回溯搜索的遍历过程:我怎么找答案。先根据for横向遍历摞一格,再根据递归纵向遍历直到叶子节点。每一颗树都是这样。
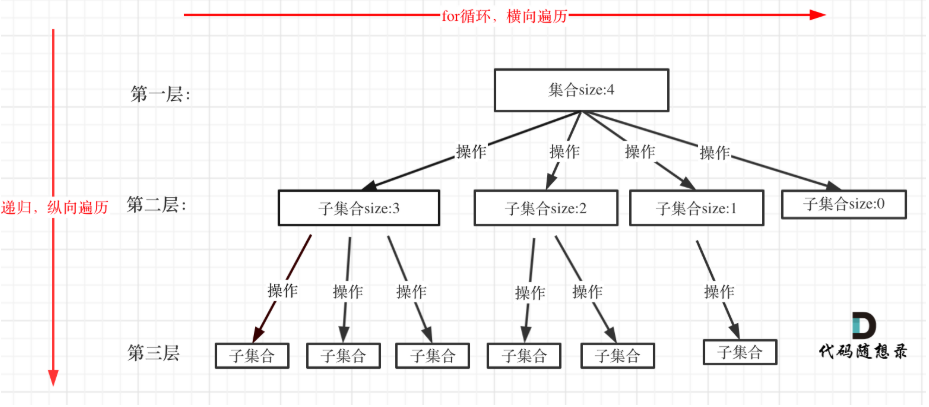
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
for循环就是遍历集合区间,就是横向遍历,可以理解一个节点有多少个孩子,这个for循环就执行多少次。
backtracking这里自己调用自己,实现递归,就是纵向遍历。
看到回溯的题目先想树是个什么样的结构。
2.组合问题 数组
39题 能重复 40题 不能重复,要去重😚
这两题都高频。
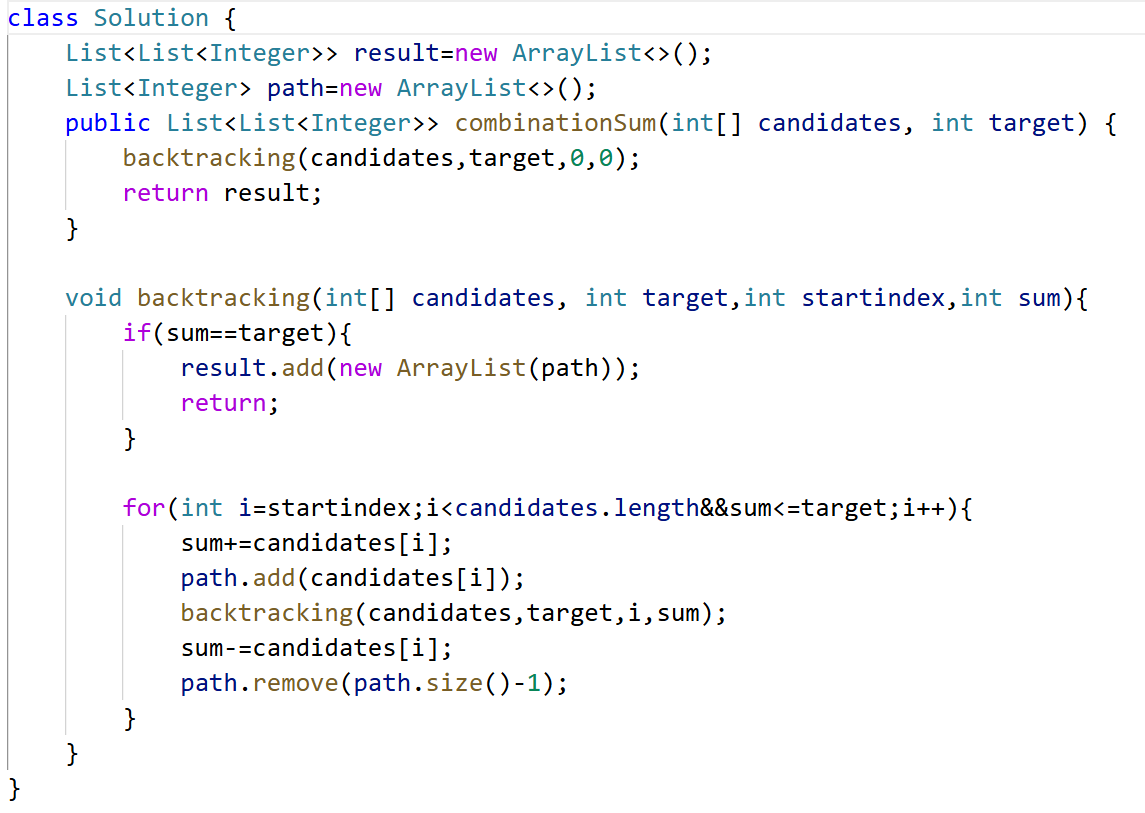
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
最后要给出的是一个数组,并且组合之间没有相关性。所以只能暴力回溯。
要从 a 中选取组合,a是主体,所以a里的东西构成树的横向和纵向。
横向是for循环,a中有几个元素,横向就是几个。
纵向是调用了回溯几次,就是递归部分,这个没有固定的长度,停下的条件有两个:
1.已经满足了目标或者已经不可能满足了(剪枝操作)。
2.递归到无法继续选择有效数字(本题组合中的数可以无限制被选取所有没有这个条件)。但是,如果不允许数字重复选取,在代码中通过 i + 1来控制每次选择的范围,就不用在递归终止这额外考虑了。
目标是要选a中和为b,所以b决定最后所有组合被选中的条件。
注意:
忘记排序:导致无法提前剪枝,效率大幅降低 。Arrays.sort(candidates);
错误传递start:传i+1会导致数字不能重复使用
浅拷贝问题:未new ArrayList直接add(path)会导致结果被修改。如果result.add(path);这样添加的是path的引用地址,后续path数值变化,result的结果也变化。 所以需要new ArrayList<>(path) 来创建 path 的副本,保存当前path的值。
backtracking(result,list,candidates,target,sum+candidates[i],i+1);去重的时候,sum+candidates[i],因为是对当前数据求和。
39 输入数组可以重复拿
for里必须得是i<candidates.length&&sum<=target。要有后面那个剪枝条件,否则不小心超了就会一直递归导致栈内存爆了StackOverflowError。
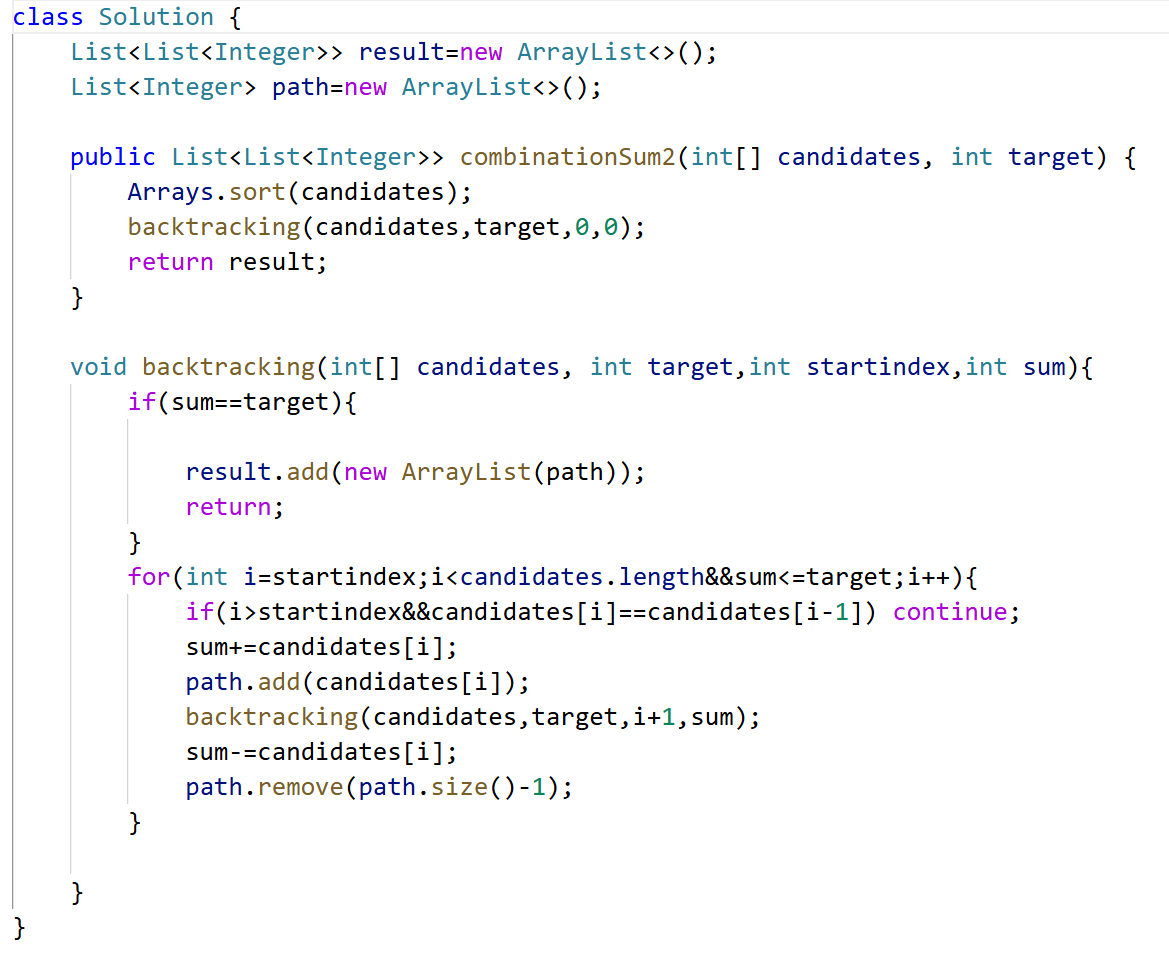
40 输入数组的数字在每个组合中只能用一次+解集不能有重复的组合
💥输入数组没说不重复,就要先进行排序Arrays.sort(candidates);。
💥 for里递归式backtracking(candidates,target,sum,i+1);可以保证输入数组的数字在每个组合中只能用一次
💥for里if(i>startindex&&candidates[i] == candidates[i-1]) continue; 可以保证解集不能有重复的组合
其余和39一样。
17题 电话号码的字母组合😚
高频。
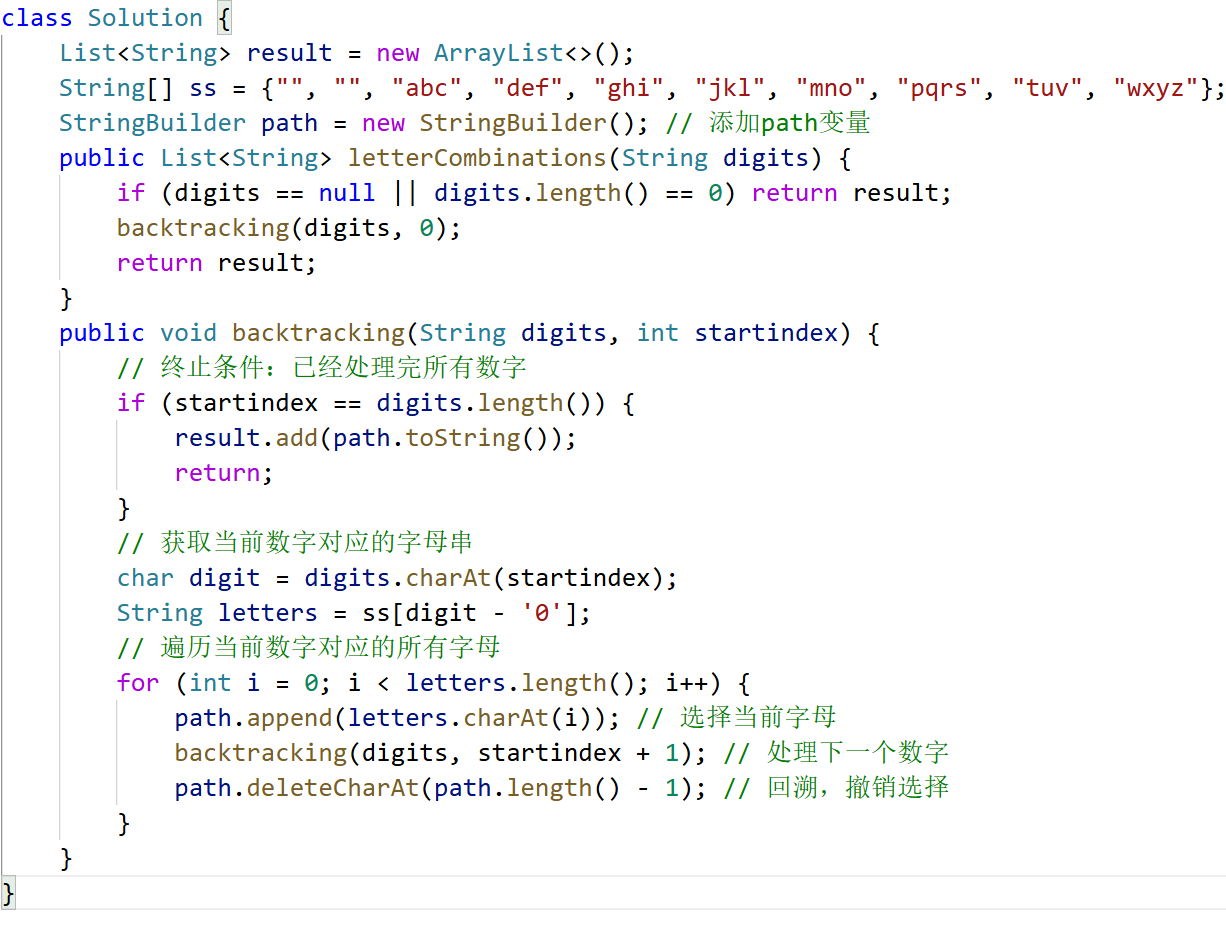
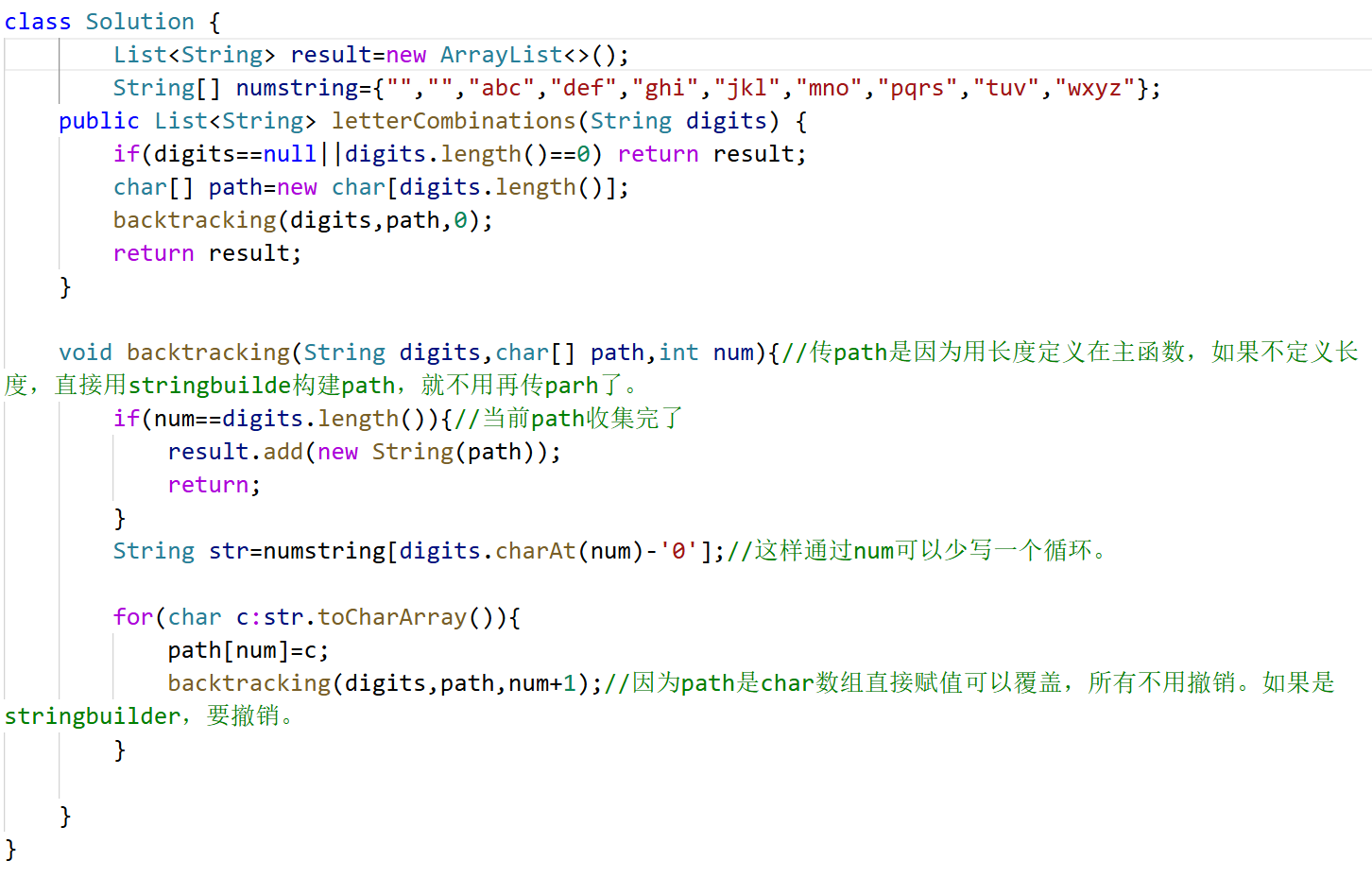
22题 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
因为path数组可以直接覆盖,所以不用恢复现场。
有效括号肯定是先左括号再右括号。
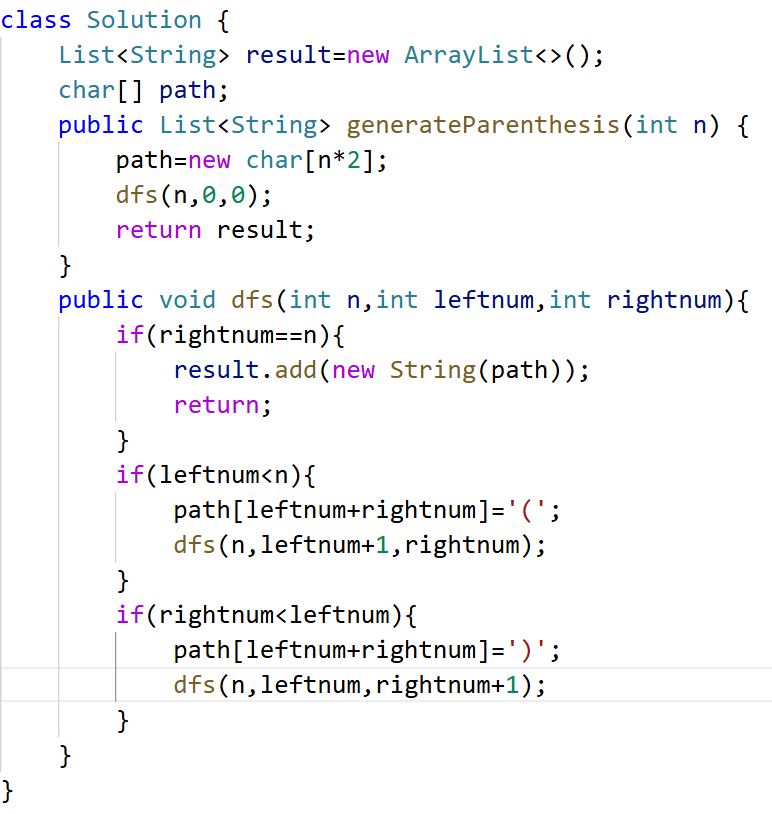

组合模板
主函数:
1.在主函数外面 先创建两个变量:二维数组result,一维数据path。
2.对a数组进行排序。
3.调用回溯函数。
4.返回结果。
回溯函数:
先if 再for。
if是筛选判断,递归终止条件,add,return。注意add的是new ArrayList<>(path),而不是path。先if就表明了无论递归到哪了,只要满足就记录答案。
for小括号里是横向遍历,遍历a的元素,记得i从index开始;
for大括号里先剪枝再添加节点到path组合里,再递归调用回溯,最后remove前面path里添加的节点,使用path.remove(path.size() - 1)这是list类通用的。
注意递归的index 从i开始表示可以重复取,从i+1开始表示不可以重复取。剪枝就是if不可能是目标组合了,就break。
注意最后的remove代表着回退,其目的是 让当前分支结束后,能够回到父节点状态尝试其他分支。
需要去重:
40题要求 candidates 中的每个数字在每个组合中只能使用一次,candidates的元素是有重复的,最后解集不能包含重复的组合。
如果只是要求candidates的数只能使用一次,那么让递归的时候回溯函数中的index从i+1开始就够了。
但是它还要求有重复的原数组里选出不能重复的解集,这里有两种解决方法:
1.加一个bool型数组used,用来记录同一树枝上的元素是否使用过。
2.剪枝,在for大括号里
if ( i > index && candidates[i] == candidates[i - 1] ) { //i > index是因为没有这个i-1就不合法
continue; //如果同一层里当前元素和前一个元素相同,就跳过当前元素,继续下一次循环。
}
3.切割问题 字符串
字符串切割两种方法,
1用StringBuilder 2用substring变换上下限。 感觉substring更简单些,记住它是左闭右开。
判断的条件可以单写一个布尔类型的函数。
131.分割回文串
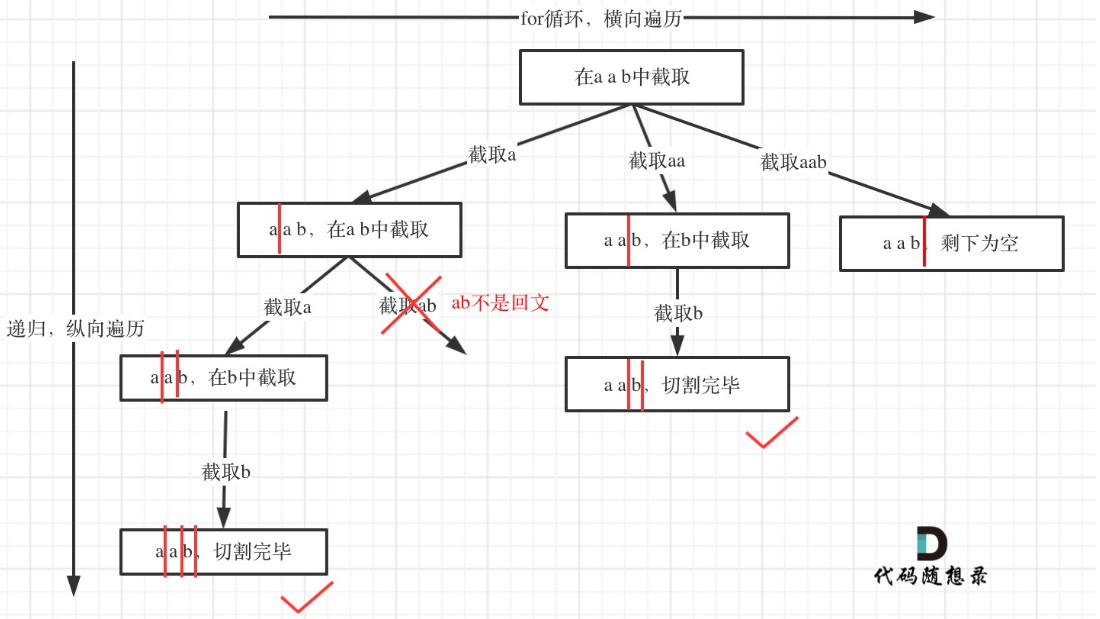
注意 是截取。
怎么切割,用切割线,也就是递归参数传入startIndex,表示下一轮递归遍历的起始位置。截取子串就是[startIndex, i]
判断一个字符串是否是回文:可以使用双指针法,一个指针从前向后,一个指针从后向前,如果前后指针所指向的元素是相等的,就是回文字符串了。
方法一用substring
注意substring是左闭右开。
终止条件是到字符遍历到最后一个,也就是处理完了整个字符串。 startindex从0开始,但由于递归是backtracking(s,i+1);所以到最后就是s的长度(+1了)。切割->递归后的startindex就是上一刀的末尾+1
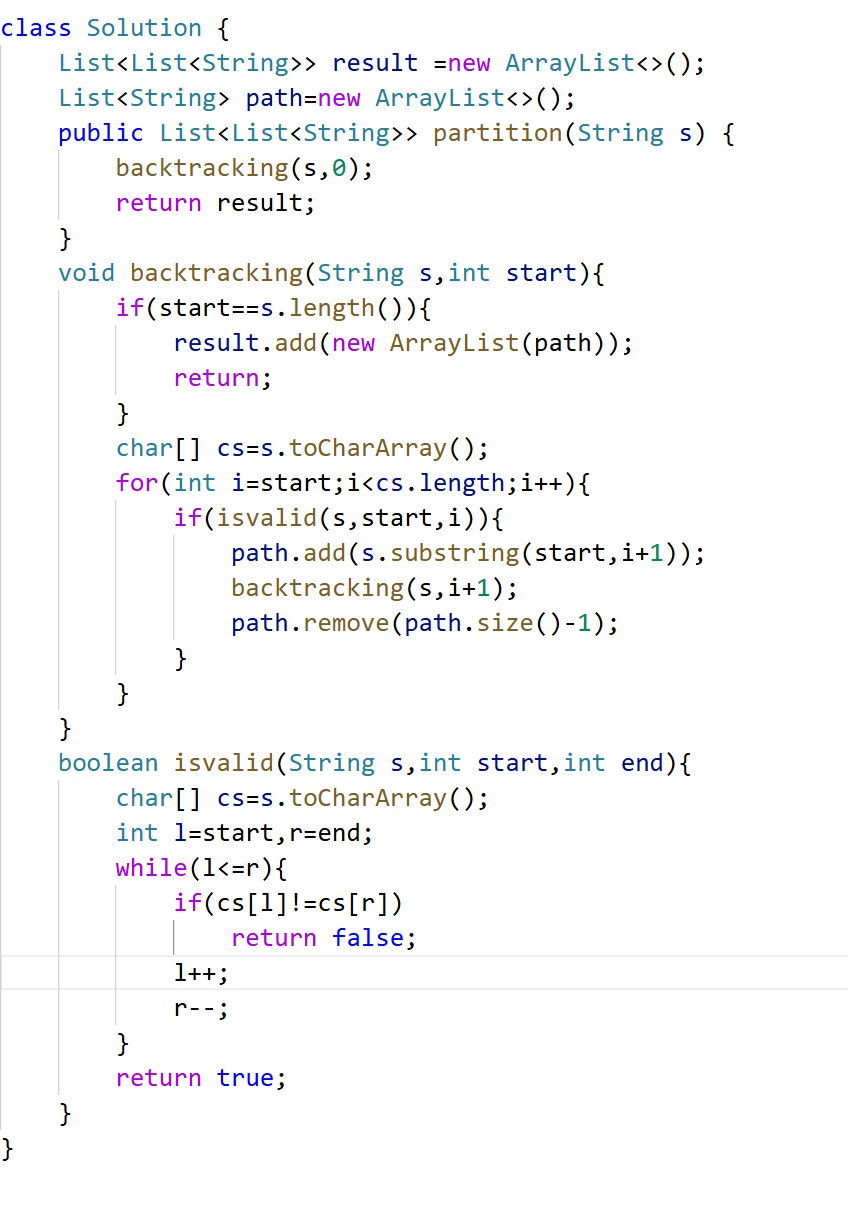
方法二用StringBuilder
也就是回溯函数里for处理节点变了,用sb可变的字符串当路径结果。
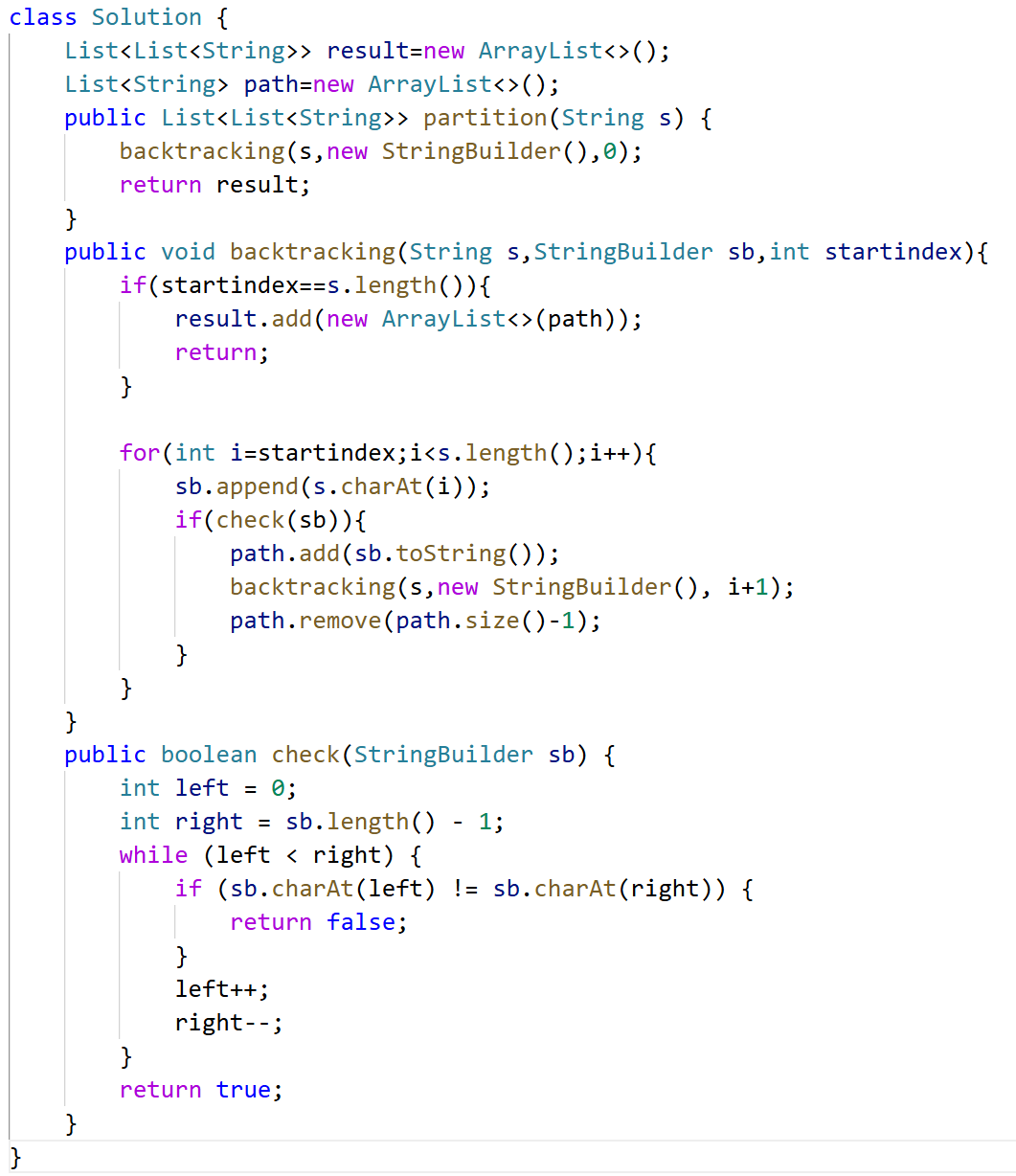
class Solution {
List<List<String>> result=new ArrayList<>();
List<String> path=new ArrayList<>();
public List<List<String>> partition(String s) {
backtracking(s,new StringBuilder(),0);
return result;
}
public void backtracking(String s,StringBuilder sb,int startindex){
if(startindex==s.length()){//在递归到达字符串末尾时,保存当前路径的副本作为
result.add(new ArrayList<>(path));
return;
}
for(int i=startindex;i<s.length();i++){
sb.append(s.charAt(i));//sb是string,所以append
if(check(sb)){
path.add(sb.toString());//path是list,所以是add。里面类是string,如果直接加sb,sb是StringBuilder就是可变的。如果有toString,那就将可变字符串内容转化为不可变字符串后保存了。
backtracking(s,new StringBuilder(), i+1);//递归时传入新的 StringBuilder 是为了:隔离不同层的选择:每层递归处理独立的子串片段;避免跨层污染:防止上层递归修改影响下层处理
path.remove(path.size()-1);
}
}
}
public boolean check(StringBuilder sb){
for(int i=0;i<sb.length()/2;i++){
if(sb.charAt(i)!=sb.charAt(sb.length()-1-i)) return false;
}
return true;
}
}
93. 复原 IP 地址 😚
好题。高频
substring写法
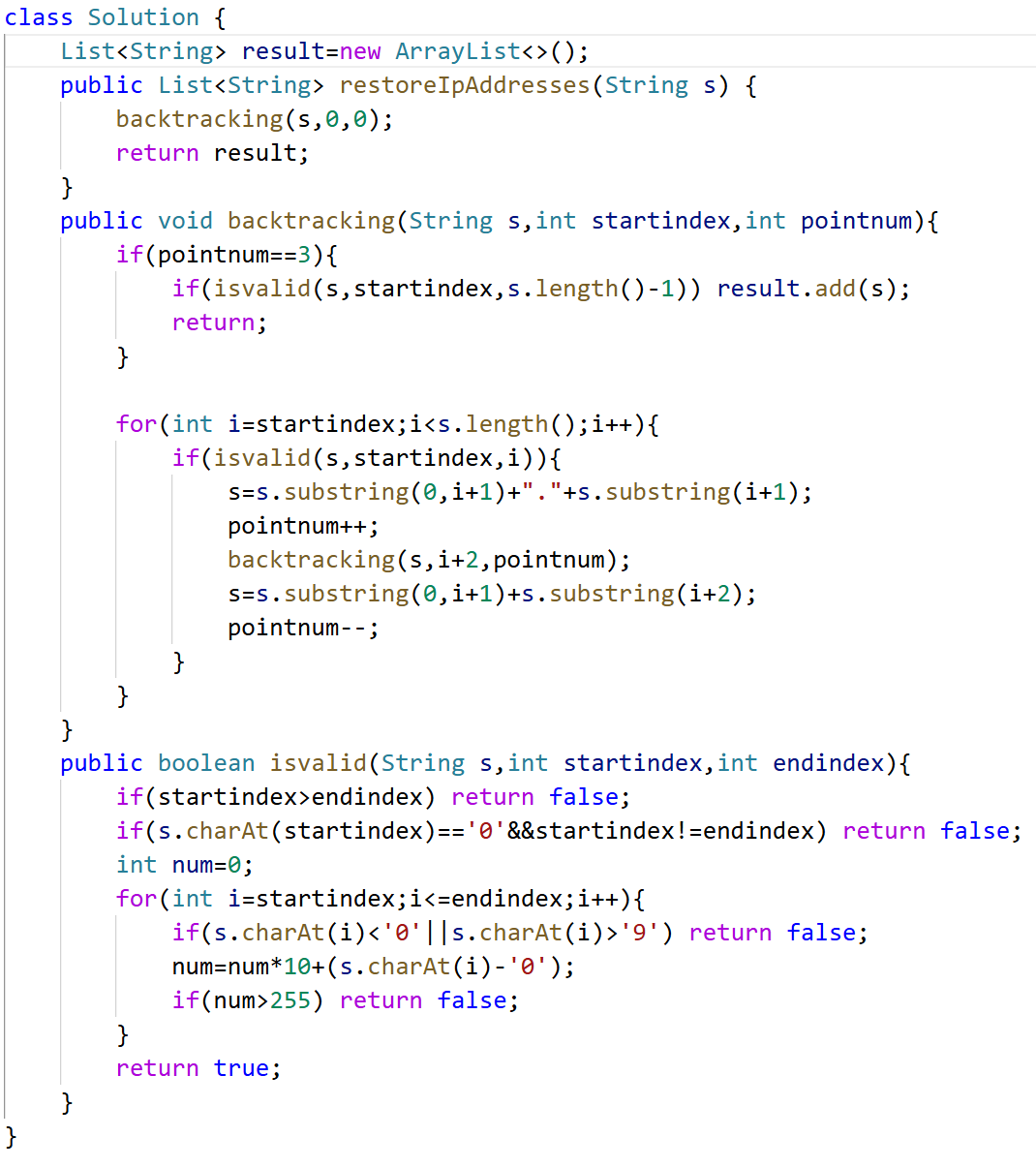
class Solution {
List<String> result= new ArrayList<>();
public List<String> restoreIpAddresses(String s) {
if (s.length() > 12) return result; // 算是剪枝了
backtracking(s,0,0);
return result;
}
public void backtracking(String s,int startindex,int pointnum){
if(pointnum==3){
if(isvalid(s,startindex,s.length()-1)){
result.add(s);
}
return;
}
for(int i=startindex;i<s.length();i++){
if(isvalid(s,startindex,i)){
s=s.substring(0,i+1)+"."+s.substring(i+1);//subString左闭右开,光写左边不写右边就是截取剩余所有的。
pointnum++;
backtracking(s,i+2,pointnum);// 插入逗点之后下⼀个子串的起始位置为i+2
pointnum--;
s=s.substring(0,i+1) + s.substring(i + 2);//删掉逗号
}else{
break;
}
}
}
// 判断字符串s在左闭右闭区间[start, end]所组成的数字是否合法
private boolean isvalid(String s,int startindex,int endindex){
if(startindex>endindex) return false;
if(s.charAt(startindex)=='0' && startindex!=endindex) return false;//单个0合法,但是01这种就不合法
int num=0;
for(int i=startindex;i<=endindex;i++){
if(s.charAt(i)<'0'||s.charAt(i)>'9'){
return false;
}
num=num*10+(s.charAt(i)-'0');
if(num>255) return false;
}
return true;
}
}
4.子集问题
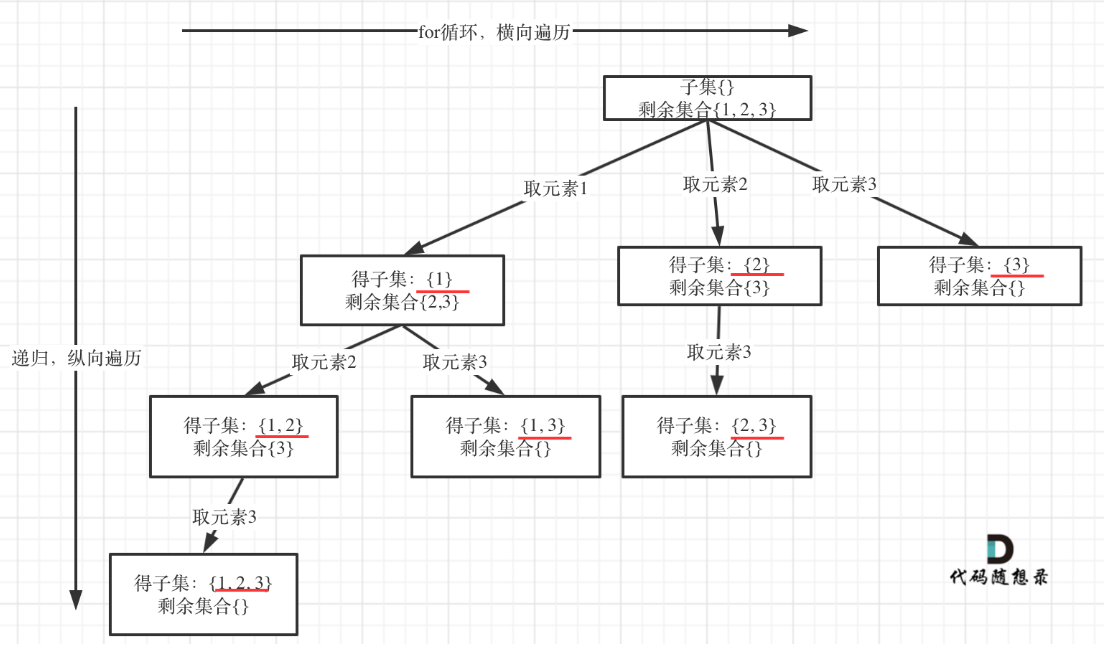
如果把 子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!其实子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和 子集{2,1}是一样的。
跟组合差不多:78子集 90子集2要求结果去重 491子集问题特殊去重。
子集模板
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
backtracking(nums,0);
return result;
}
public void backtracking(int[] nums,int startindex){
result.add(new ArrayList<>(path));// 收集子集,要放在终止添加的上面,否则会漏掉自己
if(startindex>=nums.length) return;
for(int i=startindex;i<nums.length;i++){
path.add(nums[i]);
backtracking(nums,i+1);
path.remove(path.size()-1);
}
}
}
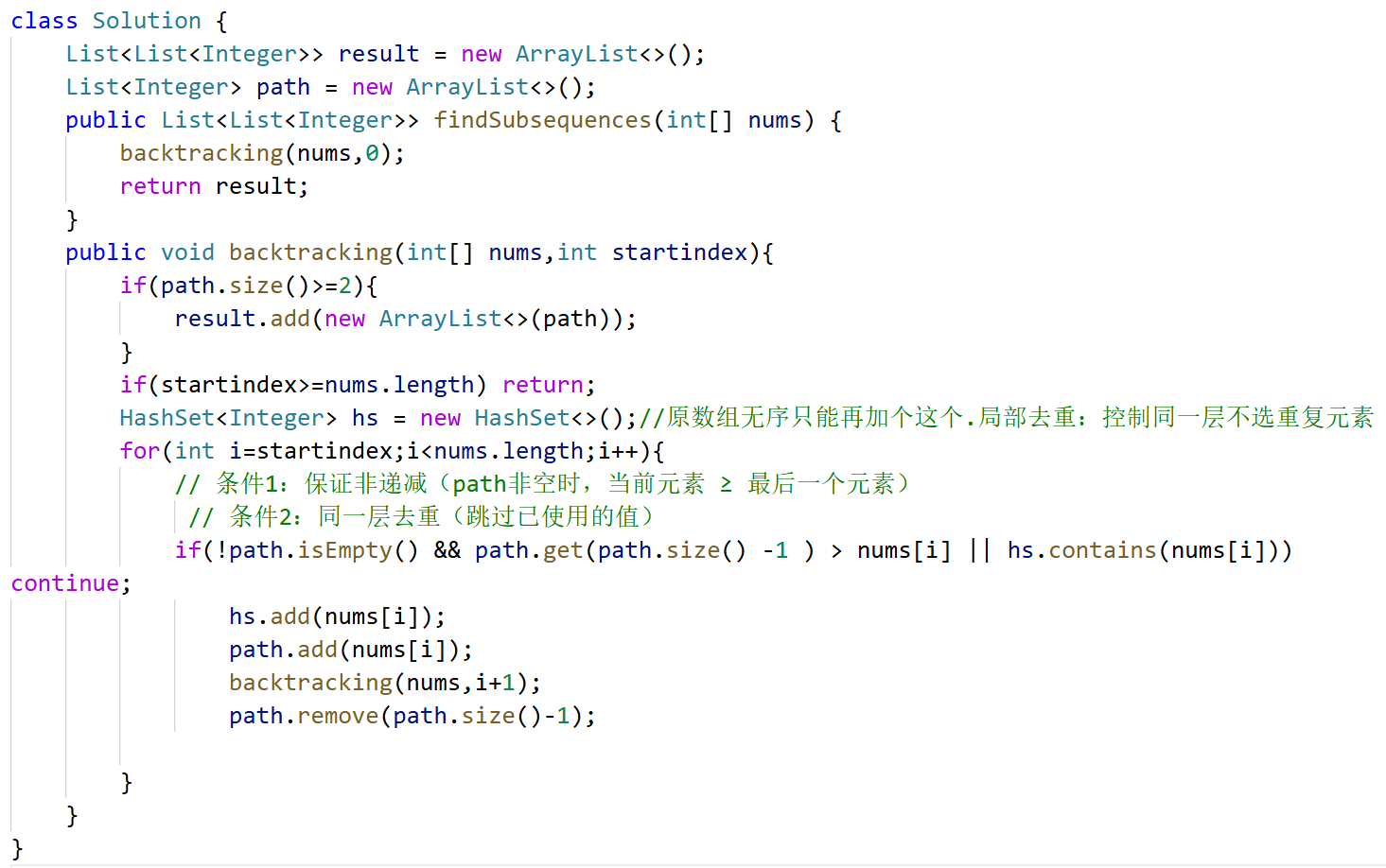
78子集😚
高频
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
注意没有终止条件,每次递归都返回。
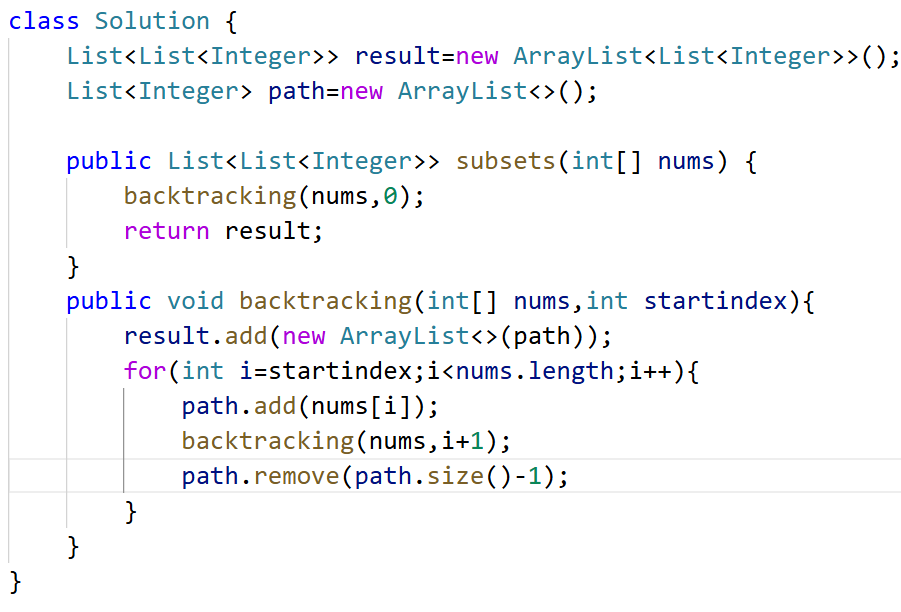
491 非递减子序列 哈希记录值来在同一层去重
本题求自增子序列,是不能对原数组进行排序的,排完序的数组都是自增子序列了。
因为这题不能排序,所以必须用哈希记录出现过的元素来进行去重。
考的概率很低。
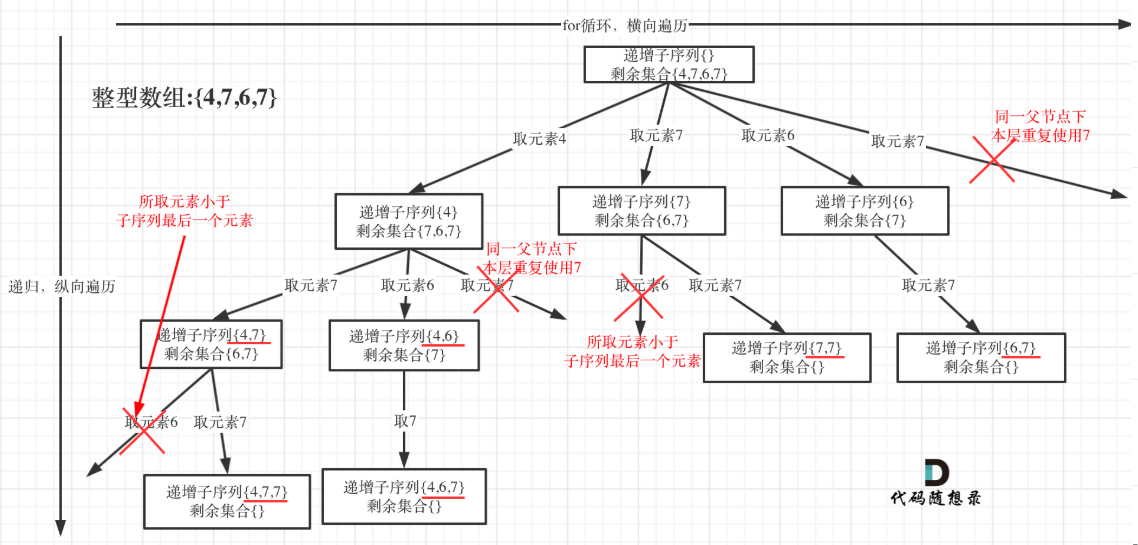
为什么可以用哈希记录一层之内的数后不用清零吗?那下层的数据怎么和上层的区分

5.排列问题
首先排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
但排列问题需要布尔类型的used数组,记录此时path里都有哪些元素使用了,因为一个排列里一个元素只能使用一次。
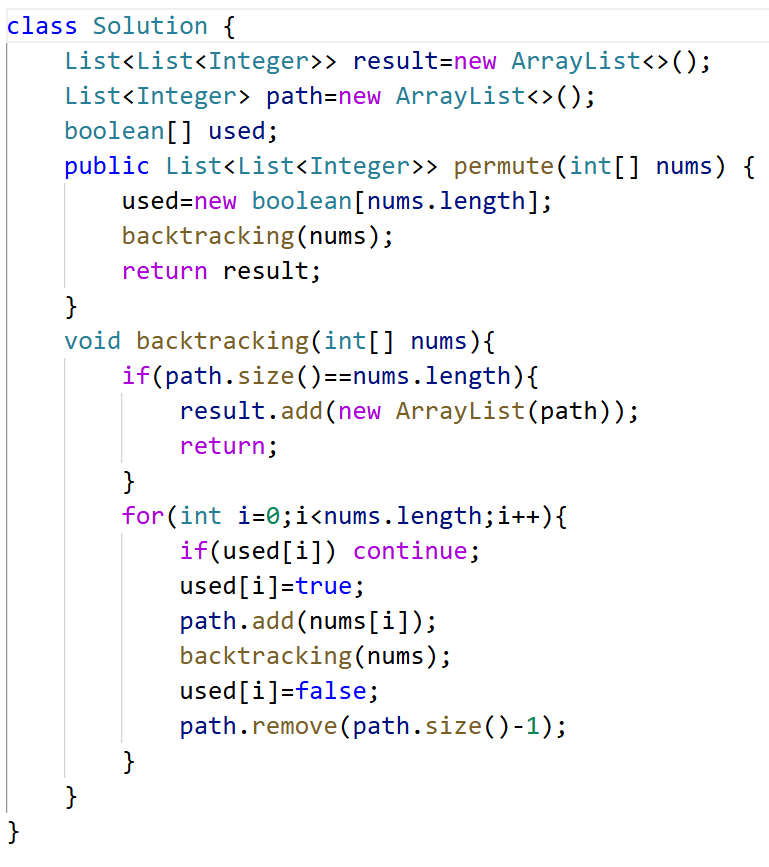
46.全排列 输入数组不含重复的 😚
简单基础。高频
排列一定要用used数组,在处理节点的时候和path加/删 一同行动。如果是如果true说明这次path用过这个数了就要continue跳过。
class Solution {
List<List<Integer>> result =new ArrayList<>();
List<Integer> path=new ArrayList<>();
boolean[] used;
public List<List<Integer>> permute(int[] nums) {
if (nums.length == 0){
return result;
}
used= new boolean[nums.length];
backtracking(nums);
return result;
}
public void backtracking(int[] nums){
if(path.size()==nums.length){
result.add(new ArrayList<>(path));
return;
}
for(int i=0;i<nums.length;i++){
if(used[i]) continue;
used[i]=true;//用到哪个,就标注一下。
path.add(nums[i]);
backtracking(nums);
path.remove(path.size()-1);
used[i]=false;//不用了也标注一下。
}
}
}
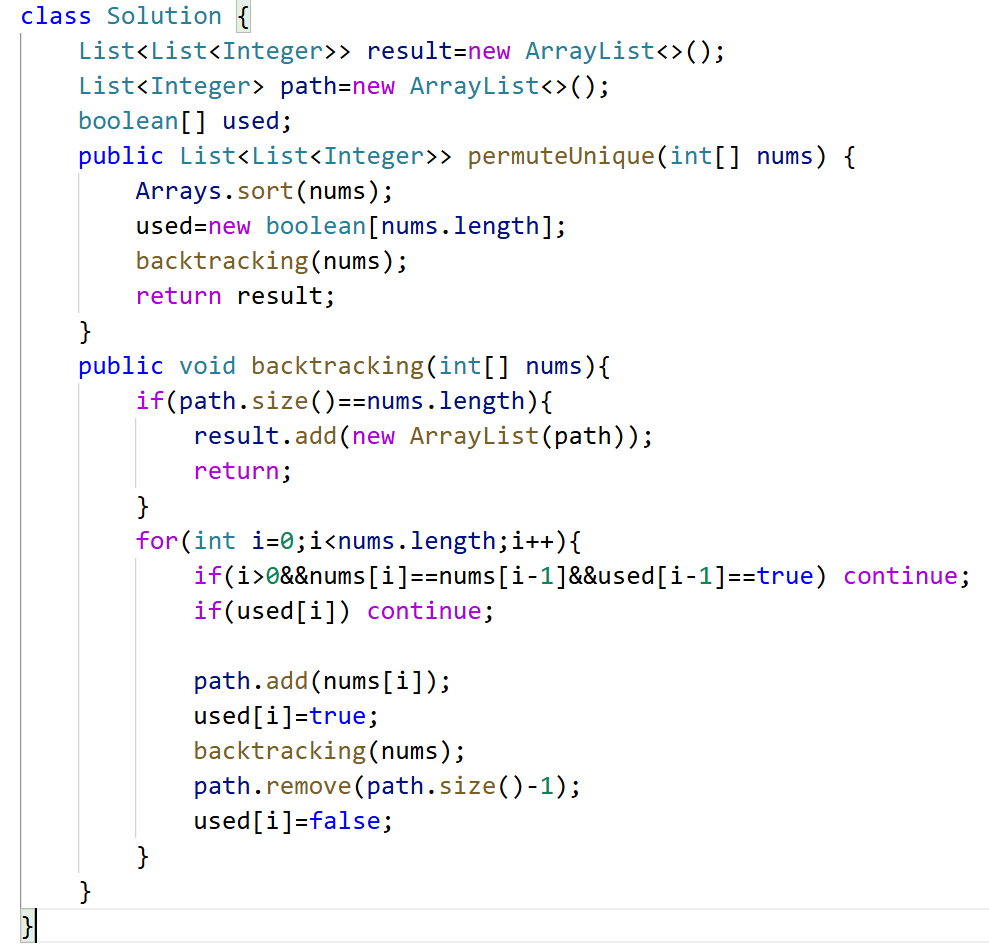
47.全排列二 输入数组有可能包含重复的,要求结果不重复的。
核心就下面这一行,其余都和46一样。去重别忘了还要used[i-1]== true
if(used[i]||(i>0&&nums[i]== nums[i-1]&&used[i-1]== true)) continue;
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> path=new ArrayList<>();
boolean[] used;
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
if(nums.length==0) return result;
used = new boolean[nums.length];
backtracking(nums);
return result;
}
public void backtracking(int[] nums){
if(path.size()==nums.length){
result.add(new ArrayList<>(path));
return;
}
for(int i=0;i<nums.length;i++){
if(i>0&&nums[i]==nums[i-1]&&used[i-1]==true) continue;
if(used[i]==false){
used[i]=true;
path.add(nums[i]);
backtracking(nums);
used[i]=false;
path.remove(path.size()-1);
}
}
}
}
回溯都是深度遍历。used添加后,递归会返回到第一层,靠的就是used false和path remove那两句。
回到第一层了,used又被重置为全false了,再根据for进行横向遍历摞一位再纵向遍历到叶子节点进行判断。
332. 重新安排行程
即给定一组机票(出发地 → 目的地),从 “JFK” 开始,按字典序返回最小的行程路线。
因为有要求有且只能用一次票,所以要用used标注。
6.棋盘问题
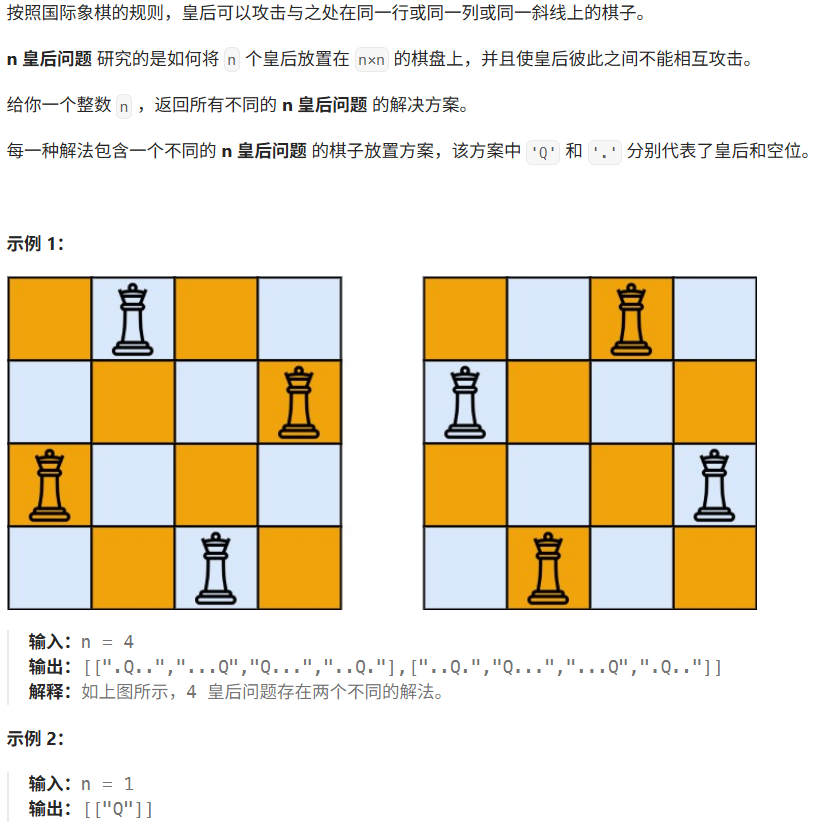
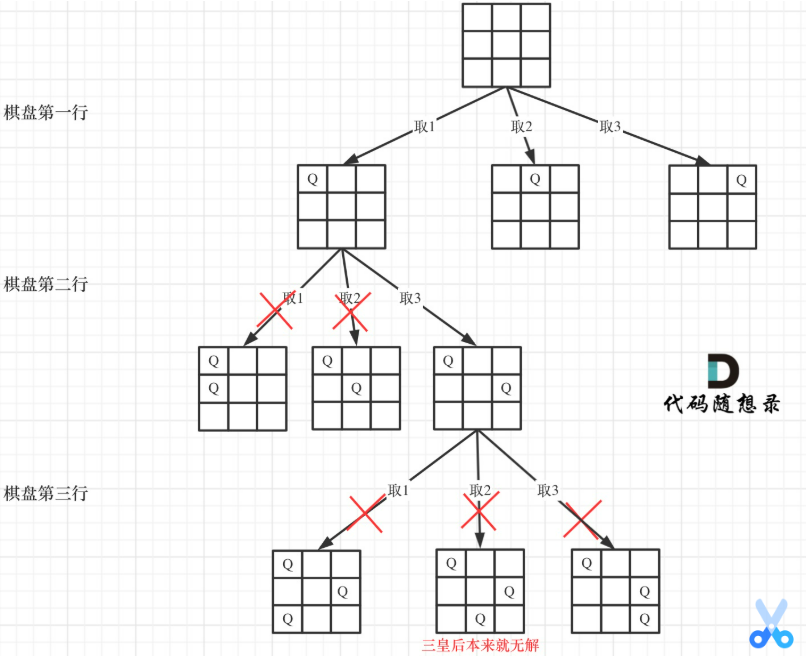
51 N皇后问题 😚
中频
一行只有一个q,一列只有一个q,斜线上也最多一个q。

class Solution {
List<List<String>> result = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
char[][] chessboard=new char[n][n];
for(char[] c:chessboard){
Arrays.fill(c,'.');
}
backtracking(n,0,chessboard);
return result;
}
public void backtracking(int n,int row,char[][] chessboard){
if(row==n){
result.add(Array2List(chessboard));
return;
}
for(int col=0;col<n;++col){
if(isvalid(row,col,n,chessboard)){
chessboard[row][col] = 'Q';
backtracking(n,row+1,chessboard);
chessboard[row][col]='.';
}
}
}
//将一个二维字符数组 char[][] chessboard 转换为一个 List<String>
public List Array2List(char[][] chessboard) {
List<String> list = new ArrayList<>();
for (char[] c : chessboard) {
list.add(String.copyValueOf(c));//将字符数组 c 转换为一个新的 String 对象。
}
return list;
}
public boolean isvalid(int row,int col,int n,char[][] chessboard){
// 检查列
for(int i=0;i<row;++i){
if(chessboard[i][col]=='Q') return false;
}
// 检查45度对角线
for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--){
if(chessboard[i][j]=='Q') return false;
}
// 检查135度对角线
for(int i=row-1,j=col+1;i>=0&&j<=n-1;i--,j++){
if(chessboard[i][j]=='Q') return false;
}
return true;
}
}
37 解数独😚
中频
class Solution {
public void solveSudoku(char[][] board) {
backtracking(board);
}
//1. 遍历所有格子 2. 尝试填入数字 1-9。递归尝试,如果递归失败,回溯,撤销填入的数字
public boolean backtracking(char[][] board){
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if(board[i][j] !='.') continue;//跳过已填数字的格子
for(char k='1';k<='9';k++){
if(isvalid(i,j,k,board)){
board[i][j]=k;
if(backtracking(board)) return true;/// 如果找到合适一组立刻返回。
board[i][j]='.';//如果找不到合适的,要恢复棋盘状态
}
}
return false;
}
}
return true;
}
/**
* 判断棋盘是否合法有如下三个维度:
* 同行是否重复
* 同列是否重复
* 9宫格里是否重复
*/
private boolean isvalid(int row,int col,char val,char[][] board){
//检测同行有没有重复的
for(int i=0;i<9;i++){
if(board[row][i]==val) return false;
}
//检测同列有没有重复的
for(int i=0;i<9;i++){
if(board[i][col]==val) return false;
}
//检测9宫格里有没有重复的
int startrow=row/3*3;
int startcol=col/3*3;
for(int i=startrow;i<startrow+3;i++){
for(int j=startcol;j<startcol+3;j++){
if(board[i][j]==val) return false;
}
}
return true;
}
}
79 单词搜索😚
高频。